前回の続きです。
超高輝度赤色LEDを使用したLEDアレイができたところで、「リヤセンターフォグランプユニット」に組み込む準備をします。

まずは、小学生の時から御用達の“工作用紙”を使って、「リヤセンターフォグランプユニット」内部の採寸をします。
天地高さは、40mmを確保できそうです。
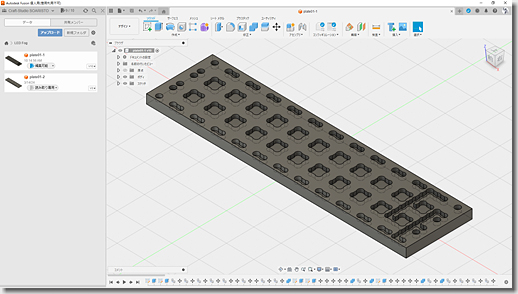
見当が付いたところで、いつものとおり、Autodesk Fusion 360でサクッと設計します。
 | ||
前回の続きです。
超高輝度赤色LEDを使用したLEDアレイができたところで、「リヤセンターフォグランプユニット」に組み込む準備をします。

まずは、小学生の時から御用達の“工作用紙”を使って、「リヤセンターフォグランプユニット」内部の採寸をします。
天地高さは、40mmを確保できそうです。

見当が付いたところで、いつものとおり、Autodesk Fusion 360でサクッと設計します。
以前の「FIA準拠・超高輝度LEDレインライト」の続編です。
ドイツから、航空小包が届きました。

Audi R8の部品ですが、VolksWagenグループだけあって、同グループ各社のロゴが入った箱に入っていました。

(画像は、天地逆さまです)
画像のとおり、「リヤセンターフォグランプユニット」(部品コード:420 945 703)です。
前回の続きです。
「Gran Turismo DD Proがやってきたっ!!」(2024年2月10日)
McLaren Automotiveの正式ライセンスを受けて製品化された、McLaren GT3のステアリングホイールのレプリカです。
本物のCAD情報を元に作られているため、レプリカと言えど、再現性は抜群(らしい)です。
Fanatecのハンコンに取り付ける、McLaren GT3のステアリングホイールですが、わたくしが、そのまま使うはずもなく・・・。
標準の状態では、パネル右下に、Xbox用のボタンなどが付いていて、このままではPlaySation 5では使いづらい感じです。

「CSL Elite Steering Wheel McLaren GT3 V2」には、付属品として、交換用のボタンや示名条片(ラベル)が付いていますが・・・。
う~ん、いまいち。
#「示名条片」って、電電用語か?0xF9C7
前回の続きです。
またも、散在してしまいました。0xF9F8

Fanatecから、総計8個もの小包が。
海外配送なので、1~2週間は掛かるだろうと思っていたのですが、注文してからわずか2日で届いてしまいました。しかも、ゆうパックで。
注文後、確認のメールが来て、
「配送手続きに入った。これ以降はキャンセルできない。追って追跡番号を知らせる」
とのことで、
「配達日は、追跡番号が分かってから、奥さんのいない日にしよう」
と余裕をこいていたのですが、まさかの瞬達。0xF9C7
どうやら、国内にストック拠点があったようです。
と、いうことで、奥さんにブツブツ言われながら運び込んで、開梱。0xF9FC

まずは、ハンコン(ハンドルコントローラー)本体、「Gran Turismo DD Pro (8Nm)」です。
フォースフィードバックが8NmのDDホイールベースに、Gran Turismo 7用のステアリングホイールやペダルなどがセットになっているものです。
本当は、セット品ではなく、8NmのDDホイールベースを単体(89,999円)買い、好みのステアリングとペダルを組み合わせたかったのですが(後述)、現時点で、DDホイールベース単体が欠品(2024年4月2日以降配送予定)で、
「そんなに長く待てないっ!!」
ということで、無駄を承知で購入しました。
ちなみに、GT7公式HPに掲載されている「Gran Turismo DD Pro Premium Bundle」(128,900円)は、現時点では、Fanatec公式HPには掲載されていません。
また「Gran Turismo DD Pro (8Nm)」も、GT7公式HPでは112,900円ですが、Fanatec公式HPでは106,300円と、少し安くなっています。
いまさらながら、ですが・・・。
以前の「PS3がやってきたっ!!」が、2007年12月のことでしたので、早16年以上の月日が流れていることになります。

我が家の「ホームゲーセン」も完成し、ドライビングシミュレーターに掛ける熱もすっかり冷めたのですが、またここへ来て復活。0xF9C7
PlayStation 4を買わずして、PlayStation 5を買ってしまいました。
第一世代より小型化され、Ultra HD Blu-rayディスクドライブを内蔵している第二世代(CFI-2000A01)です。
ヨドバシカメラにて、「いまなら、スパイダーマン2同梱版が同じ価格で購入できますが、いかがですか?」と勧められましたが、「いや、結構です」とキッパリ。
#そんな子供向けの映画なんて、要るかいな。0xF9D1

目的はやはりこれ、「Gran Turismo 7」です。